Arithmetic algorithm coded in Perl
Generating $n Fibonacci numbers:####################################
for ($i=0; $i<$n; $i++)
{
# The Euler-Binet Formula
$fibonacci = (1/sqrt(5))*((1 + sqrt(5))/2)**$i
- (1/sqrt(5))*((1 - sqrt(5))/2)**$i;
# Rounding off to a whole number if necesssary
$fibonacci = int($fibonacci + 0.5);
print "$fibonacci\n";
}
####################################
The Euler-Binet Formula
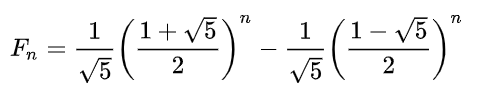
Altogether, the arithmetic algorithm based on the Euler-Binet formula will generate the sequence of 1475 Fibonacci numbers starting from 0
with the largest one being 4.99225460547801 x 10307, as opposed to 1477 Fibonacci numbers generated by the iterative method.
Importantly, the arithmetic algorithm for the Fibonacci sequence generation seems to be pretty fast and effective as compared to the recursive method.
In my benchmark test of generating 1475 Fibonacci numbers as many as 1 mln times all over again, the arithmetic algorithm proved to be 1.5 times slower than the iterative one
as evaluated by the wall-clock time consumed by each process.
Another problem is the acuracy of the arithmetic algorithm which can be questioned early enough as the method involves very heavy exponentiation (raising to the power) of the square root of five being an irrational number.
Now, why don't you go up and challenge the arithmetic algorithm yourself! I recommend that you try it specifically for n = 1476 and see what happens. Then compare the result with what you get using the iterative method (very pedagogical). 
