Algorytm arytmetyczny kodowany w Perlu
Generuj $n liczb Fibonacciego:####################################
for ($i=0; $i<$n; $i++)
{
# Wzór Eulera-Bineta
$fibonacci = (1/sqrt(5))*((1 + sqrt(5))/2)**$i
- (1/sqrt(5))*((1 - sqrt(5))/2)**$i;
# Zaokrąglenie do liczby całkowitej
$fibonacci = int($fibonacci + 0.5);
print "$fibonacci\n";
}
####################################
Wzór Eulera-Bineta
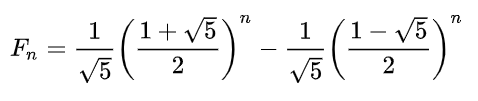
Algorytm arytmetyczny korzystający ze wzoru Eulera-Bineta jest w stanie wygenerować ciąg 1475 liczb Fibonacciego (wliczając zero)
przy czym największa liczba ciągu wynosi 4,99225460547801 x 10307, co stanowi pewne ograniczenie w porównaniu do 1477 liczb Fibonacciego generowanych metodą iteracyjną.
Na podkreślenie zasługuje fakt, że algorytm arytmetyczny generujący ciąg Fibonacciego jest bardzo szybki i efektywny w porównaniu z metodą rekurencyjną.
W moich testach wydajności polegających na generowaniu 1475 liczb Fibonacciego w cyklach powtarzanych milion razy (bez przerw pomiędzy cyklami), algorytm arytmetyczny okazał się ok. 1,5 raza wolniejszy niż iteracyjny.
Kolejnym problemem jest nieco wątpliwa dokładność algorytmu arytmetycznego związana z koniecznością zaokrąglania liczb będących wynikiem wielokrotnego potegowania liczb niewymiernych (pierwiastek z pięciu).
Zachęcam niniejszym do testowania algorytmu arytmetycznego! Proponuję spróbować wygenerować przy jego pomocy 1476 liczb Fibonacciego a następnie porównać wynik z uzyskanym metodą iteracyjną (bardzo pouczające). 
